First Linear Regression Model in R

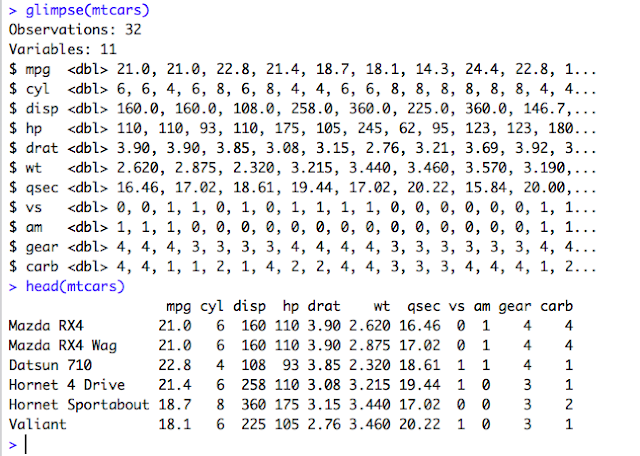
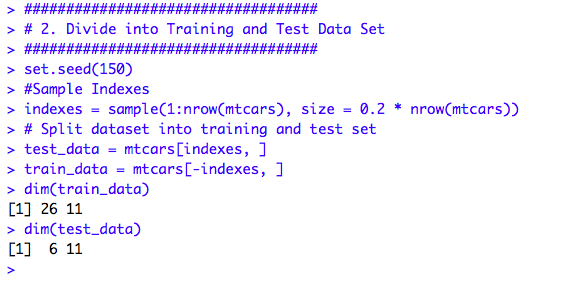
For this example, we will use the mtcars dataset, a dataset that was extracted from the 1974 Motor Trend US magazine, and comprises fuel consumption and 10 aspects of automobile design and performance for 32 automobiles (1973–74 models). Below is a brief description of the variables in the dataset:

[, 1]	mpg	Miles/(US) gallon
[, 2]	cyl	Number of cylinders
[, 3]	disp	Displacement (cu.in.)
[, 4]	hp	Gross horsepower
[, 5]	drat	Rear axle ratio
[, 6]	wt	Weight (1000 lbs)
[, 7]	qsec	1/4 mile time
[, 8]	vs	V/S
[, 9]	am	Transmission (0 = automatic, 1 = manual)
[,10]	gear	Number of forward gears
[,11]	carb	Number of carburetors

 

2. Divide into Training and Test Dataset:

The “mtcars” Dataset has 32 observations and 11 variables. Each record of mtcars represents one model of car, which we can see in the row names. Each column is one attribute of that car, such as the miles per gallon (or fuel efficiency), the number of cylinders, the displacement (or volume) of the car’s engine in cubic inches and so on.

We will divide the Dataset into a Training Set(80% of the records) and a Test Set(20% of the records). We will use the Training Set to build a Linear Regression Model and will use the Test Set to test the efficiency of the model created.

 

3. Build a Linear Regression Model:

We will build the linear relationship model using the lm() function in R.  First, we will build the model to predict “mpg”(miles/gallon) value using all the available variables in the “mtcars” Dataset.

4. Understanding the Model

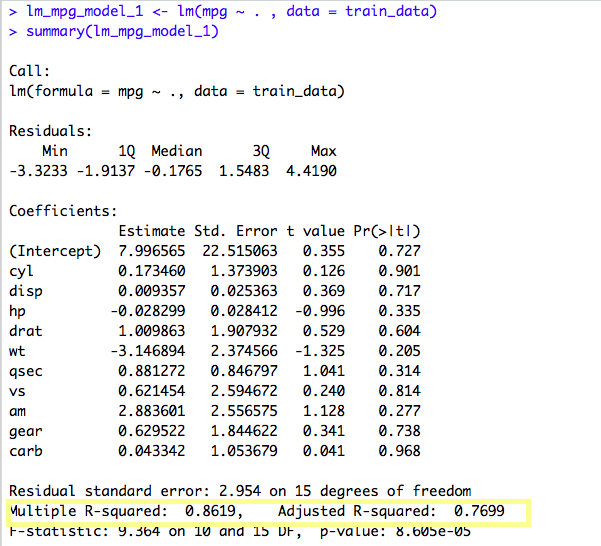
Using the summary() function on the Linear Model created, we are able to see the coefficients and some other values. Let’s summarize what we can see in the above output:

1. The independent (predictor) variables are listed on the left i.e. cyl, disp, hp, etc.
2. The Estimate column gives the coefficients for the intercepts for each of the independent variables in our model.
3. The Std. Error column gives a measure of how much the coefficient is likely to vary from the estimated value.
4. The t value column is Estimate/Std Error. It is negative if the Estimate is Negative and Positive if the Estimate is Positive. The larger the ABSOLUTE value of this variable, the more likely the coefficient to be significant. So, the higher the t-value, the better.
5. The Pr(>ltl) column gives the probability that a coefficient is actually zero. We want variables with a small value in this column.
6. There is another easy way to evaluate the significance of variables by seeing the number of stars(***) at the end of each variable. But, for the above model, we are not seeing any stars for any variable. 
7. After a Linear Regression Model is created, we need to determine how well the model fits the data. An important statistical measure is the R-squared value. R-squared is always between 0 and 100%:

• 0% indicates that the model explains none of the variability of the response data around its mean.
• 100% indicates that the model explains all the variability of the response data around its mean.

In general, the higher the R-squared, the better the model fits the data. But, every time we add a predictor to a model, the R-squared increases. It never decreases. That’s why it is better to check for another statistical measure the “Adjusted R-Squared” value. 
8. The adjusted R-squared is a modified version of R-squared that has been adjusted for the number of predictors in the model. The adjusted R-squared increases only if the new predictor variable improves the model. It is always lower than the R-squared.

Now, let’s create another model, using a few variables with a lower value in the last column.

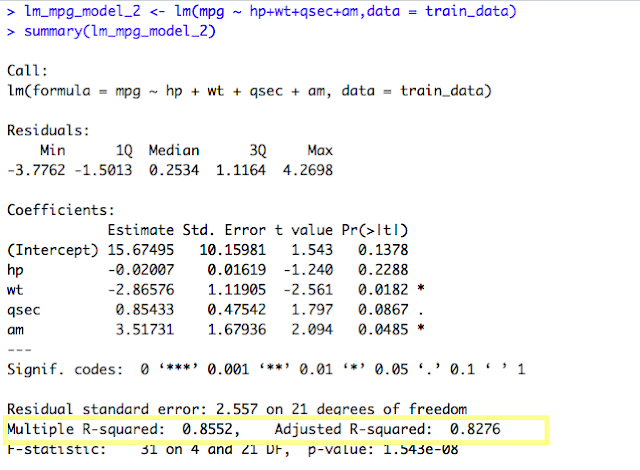
We can see a single star for the variables “am” and “wt”. There is a dot(.) for variable “qsec” . “hp” seems to have not much significance in building the Model. So, let’s create another model removing the variable “hp”. 

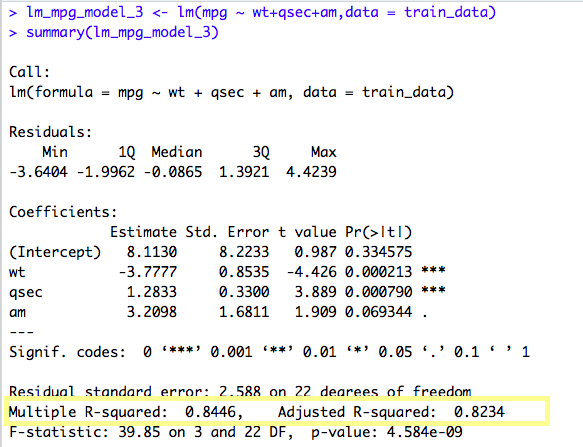
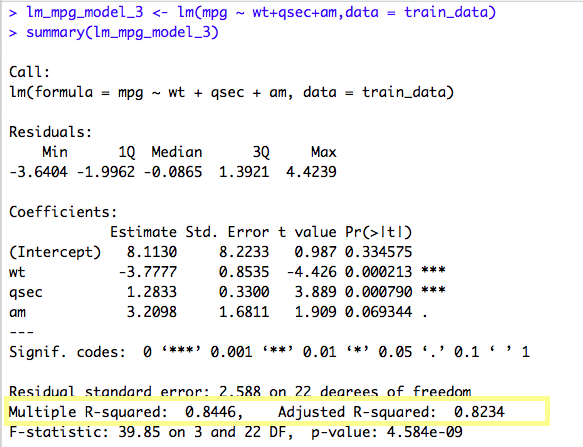
The current model, “wt” and “qsec” variable seems to have triple stars and “am” variable has a dot(.). That means, all the variables are of significant value in predicting the mpg. Also, the Adjusted R-Squared value is 0.8234 which is pretty high and thus it tells how accurate our Linear Model is.

5. Making a Prediction

We have built a Linear Regression Model to predict the miles/gallon(mpg) variable based on three input variables wt,qsec and am. We have trained our Model using the Training Data Set. Now, to make a prediction, we need the data which the Model has not seen yet. That’s why we will use our Test dataset for prediction. In R, we will use the function predict().

As per our Model, the Predicted mpg value for Mazda RX4 Wag is 22.30340 and the actual value in our Test dataset is 21.0 which is not exact but almost accurate. To test the accuracy of our Linear Regression Model, we can calculate the R-Squared value on our Test Data. The formula is
1- SSE/SST
In our case, the value is 0.89 which is pretty high and almost accurate.

6. Build a Mathematical Equation:

Let’s build a Mathematical Equation based on the model we just created. We will check the values of the coefficient for each of the predictor variables from the model just created and will create a mathematical equation using these values. We need to get a summary of the relationship model to know the average error in prediction (Also called residuals).

mpg = 8.1130 – (3.7777)*wt + (1.2833)* qsec + (3.2098) * am
Lets, consider the 1st data in the Training DataSet i.e. Mazda RX4 Wag.
Let’s Calulate:
mpg(Mazda RX4 Wag) = 8.1130 – (3.7777)*2.875 + (1.2833)*17.02 + (3.2098) * 1 = 22.30368

As per the Test Data, the actual mpg value is 21.0 and the predicted value is 22.3.
The mathematical representation of a Linear Regression Model is posted here in detail.